IN BREVE
In natura, qualunque forma di energia vibrazionale tende a distribuirsi e concentrarsi nello spettro delle frequenze secondo uno schema ben preciso e ricorrente. Se ordiniamo dalla più grave alla più acuta queste frequenze otteniamo la scala degli armonici naturali. Questa “scala” non è stata creata o decisa dall’uomo, ma è una legge di natura, è la conseguenza di un fenomeno fisico e come tale può essere spiegato in termini matematici. Il modello matematico che descrive questo schema è chiamato serie armonica.
Il modello matematico è semplice: data una frequenza fondamentale f, la serie armonica da essa generata è la successione dei suoi multipli interi (f x 1, f x 2, f x 3 …). Per semplicità queste frequenze multiple vengono dette “armoniche” o “armonici”1.
Gli armonici sono una legge di natura.
La conoscenza di questo schema ha permesso all’uomo di progredire nella scienza, nella tecnologia e trova applicazione in innumerevoli settori, dall’ingegneria alle pratiche più spirituali.
La musica è senza dubbio il campo in cui il fenomeno degli armonici si palesa più facilmente ai nostri sensi. La scala musicale derivata dalla serie armonica potrebbe essere definita la più ancestrale delle melodie che, in quanto legge naturale, è alla base di tutta la musica.
IN MUSICA
In musica le note della serie armonica possono essere “suonate” in due modi. Questi due modi si differenziano per il principio fisico con cui vengono generati gli armonici.
- Il canto armonico, gli scacciapensieri e gli archi musicali da bocca, il k’ni e il suo omologo elettrico, la talk-box.
Canto armonico (dal 4° al 16° armonico):
- I filtri elettro-acustici presenti nei sintetizzatori2.
Un filtro passa banda applicato ad un’onda a dente di sega (primi 16 armonici):
Sia i primi che i secondi si avvalgono di filtri risonanti3 che amplificano certe zone dello spettro armonico. Da notare che in questo modo è sempre presente la fondamentale (il tono di base), dal quale provengono gli armonici. In questo caso i toni armonici sono delle semplici sinusoidali.
- AEROFONI: I corni e le trombe naturali e i flauti armonici modificando l’intensià del soffio.
Una tromba naturale in Do (dal 4° al 20° armonico): Un flauto in Do (dal 1° all’8° armonico):
- CORDOFONI: Il Đàn bầu e in genere tutti gli strumenti a corda, come la chitarra, se suonati con una apposite tecniche4.
Una chitarra (dal 1° al 12° armonico):
In questo caso il tono fondamentale normalmente non è udibile in quanto viene suonato solo l’armonico. In questo caso i toni armonici sono suoni più complessi e con un timbro caratteristico (e non delle semplici sinusoidali).
Guardiamo ora la serie armonica. Nel video che segue sentiamo i primi 17 armonici generati artificialmente con un software (Overtone Analyzer). Al contrario dei reperti audio precedenti che erano in Do, questa volta è in La (220 Hz).
Differenze con la musica occidentale
Gli intervalli (note) musicali “suonabili” con il canto difonico non corrispondono esattamente agli intervalli usati dalla musica convenzionale occidentale, basata sul sistema di temperamento equabile (12-TET).
I primi tre armonici però li riscontriamo in quasi tutte le culture, e anche nel sistema equabile.
Unisono, ottava e quinta possono essere definiti degli universali culturali (con rarissime eccezioni per la quinta)5.
I primi 3 armonici sono gli intervalli di unisono, ottava e quinta.
- Unisono6: la frequenza fondamentale (es. Do1)
- Ottava: il doppio della frequenza fondamentale (es. Do2)
- Quinta: il triplo della frequenza fondamentale (es. Sol2)
Oltre a questi, ogni popolo e cultura nel corso della storia ha sviluppato dei propri sistemi per determinare gli altri intervalli.
Musicisti, filosofi e matematici da millenni discorrono su quale sia il miglior modo per “suddividere una corda”.
Seguono alcuni importanti sistemi di accordatura attualmente riconosciuti ed utilizzati nel mondo:
Temperamento equabile
Just intonation
Serie degli armonici naturali
Non è un vero e proprio sistema di accordatura, in quanto non è una convenzione come i precedenti, ma è un fenomeno universale naturale che può essere applicato in musica per individuare degli intervalli (e dunque creare melodie e accordi). Solitamente si sceglie un gruppo di armonici e da questi se ne ricava una scala (p.es. dal 4° al 8° oppure dal 8° al 16° armonico). Ad eccezione dei rapporti di Ottava e Quinta, le altre “note” non corrispondono a quelle che otteniamo con il nostro temperamento equabile.La serie armonica non è un’invenzione ma è una scoperta.
Di seguito uno schema che esemplifica la struttura della serie armonica in musica:

I primi 32 armonici – © by armonici.it (CC BY-NC-SA)
I numeri romani indicano le ottave. Quindi tra l’armonici 1, 2, 4, 8, 16 e 32 c’è sempre l’intervallo di un’ottava.
Di seguito il numero dell’armonico con il corrispondente intervallo8 secondo la nomenclatura occidentale del sistema equabile.
| 1° | = Fondamentale (unisono) | |
| 2°, 4°, 8°, 16°, 32° | = Ottave | |
| 3°, 6°, 12°, 24° | = Quinte perfette | |
| 5°, 10°, 20° | = Terze maggiori (calanti) | |
| 7°, 14°, 28° | = Settime minori (calanti) | |
| … | … |
La sequenza degli intervalli nella serie armonica è sempre il medesimo, qualunque sia il tono fondamentale. Per esempio tra il 2° e il 3° armonico c’è sempre una quinta perfetta, e tra il 4° e il 5° una terza maggiore (un po’ calante) .
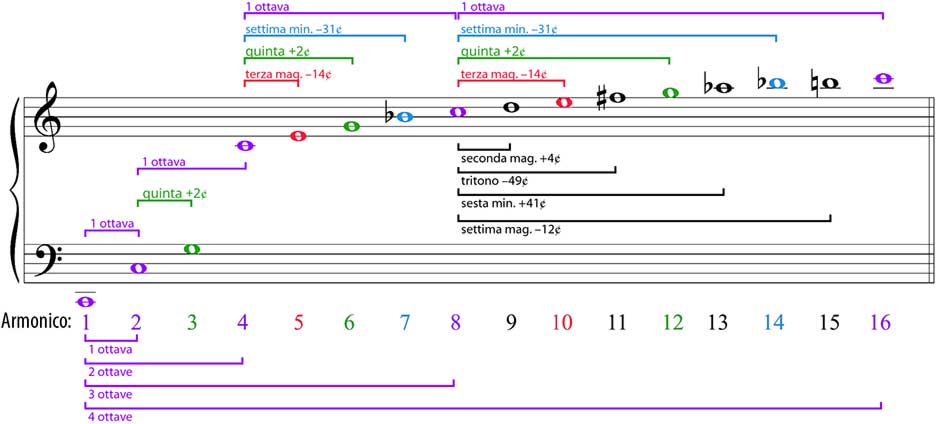
Per chi trova più familiare il pentagramma seguono i primi 16 armonici nella loro estensione di 4 ottave. Ho aggiunto dei riferimenti per indicare l’intervallo di ciascun armonico ripetto alle ottave della fondamentale. Sono indicati gli scarti in cent (¢) rispetto al nostro sistema equabile (12-EDO). Nell’esempio la fondamentale è un Do:
Utilizzando come fondamentale un tono di DO, questa è l’approssimazione dei primi 16 armonici rispetto al temperamento equabile.
IN MATEMATICA E FISICA
Gli armonici sono un fenomeno fisico, e l’uomo fin dall’antichità lo ha studiato con la matematica e la geometria. Come già abbiamo detto, il modello che descrive questo fenomeno è oggi chiamato serie armonica.
Intorno al 500 a.C. in Grecia, Cina e India molti sapienti si dedicano allo studio delle scienze matematiche e fisiche. Alcuni di loro notarono alune interessanti rapporti tra la fisica dei suoni e la geometria. Per esempio il nostro europeo Pitagora è celebre per le sue scoperte in geometria. Studiando le proprietà geometriche delle frazioni, egli si accorse che era molto più efficace (e divertente) sperimentarle nel mondo reale che nella propria mente: anziché disegnare un segmento e dividerlo, si poteva dividere la corda di uno strumento musicale. Così facendo si accorse che si potevano ascoltare le frazioni!
Si tramanda che Pitagora ideò uno stumento apposito per fare questi esperimenti: il monocordo, una corda in tensione posata su un ponte mobile che permette di dividere la corda a piacere e ottenere suoni di altezza (frequenza) variabile.9. Una delle prime cose che osservò fu che gli accordi tra i suoni prodotti dividendo la corda in parti uguali e dunque per numeri interi (1, 2, 3, 4, 5 …) erano più gradevoli all’udito che gli accordi tra suoni prodotti con divisioni non intere.
Frazioni di corda
Prendiamo una corda in tensione di una certa lunghezza e la dividiamo per la serie di numeri interi naturali (1, 2, 3, 4, 5 …). Otteniamo così una serie di frazioni di corda che, se fatte vibrare, generano le frequenze armoniche rispetto alla frequenza della corda intera che chiamiamo fondamentale.
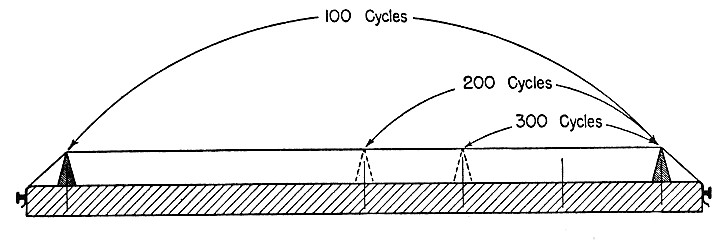
Frazioni di corda con il monocordo – by Brian Harlan and Arun Chidambaram – University of Southern California
Nell’esempio qui sopra abbiamo una corda che vibra a 100 cicli al secondo, ovvero 100 Hz. Questa è la fondamentale. Se dividiamo la corda ad 1/2 della lunghezza vibrerà al doppio della frequenza, ovvero 200 Hz. Se la dividiamo ad 1/3 della lunghezza otterremo il triplo della frequenza, ovvero 300 Hz.
Teoricamente potremmo continuare all’infinito questa divisione ed otterremo frequenze sempre maggiori in rapporto armonico con la fondamentale. L’immagine seguente può rendere bene l’idea.

Parziali armoniche di corda – by Qef [Public domain], via Wikimedia Commons
Multipli di frequenza
Prendiamo un suono, o meglio un tono, di una certa frequenza ( f ) e moltiplichiamo questo valore per la serie dei numeri interi naturali ( n ). Otteniamo così un’altra serie di numeri che rappresentano le frequenze armoniche rispetto a quella di partenza.
f = frequenza (viene misurata in Hertz [Hz])
n = numero intero naturale (1, 2, 3, 4, 5, … )
Esempio in Do:
f = 261,6 Hz è Do (C4)
fn = 261,6 Hz x n
primo armonico: f1 = 261,6Hz x 1 = 261,6Hz è Do (C4) secondo armonico: f2 = 261,6Hz x 2 = 523,2Hz è Do (C5) terzo armonico: f3 = 261,6Hz x 3 = 784,8Hz è Sol (G5) +1,96 cents10 quarto armonico: f4 = 261,6Hz x 4 = 1046,4Hz è Do (C6) quinto armonico: f5 = 261,6Hz x 5 = 1308,0Hz è Mi (E6) –13,69 cents sesto armonico: f6 = 261,6Hz x 6 = 1569,6Hz è Sol (C6) +1,96 cents settimo armonico: f7 = 261,6Hz x 7 = 1831,2Hz è Si♭ (B♭6) –31,17 cents ottavo armonico: f8 = ... ... ...
Vedi la serie armonica in matematica su Wikipedia: italiano, inglese.
 |
Questo contenuto è protetto da copyright: © 2015-2024 Walter Mantovani – Alcuni diritti riservati. |
|---|---|
| Questo contenuto è distribuito con licenza Creative Commons Attribuzione – Non commerciale – Condividi allo stesso modo 3.0 Italia. |
- Non entreremo del dibattito sull’utilizzo di un’espressione piuttosto che l’altra. In questo sito si è scelto per semplicità di usare sempre il termine “armonico” al maschile. [↩]
- Tramite il parametro resonance. [↩]
- Nella prima categoria si sfrutta la cavità orale come filtro risonante. [↩]
- Vedi la voce “Armonici artificiali” su Wikipedia. [↩]
- Gli intervalli musicali (note) derivati dai primi 3 armonici possono essere definiti un universale culturale in quanto sono gli unici intervalli che riscontriamo in tutte le culture. Mi hanno riferito di rarissime eccezioni per il 3° armonico, ma in merito non ho ancora trovato un riferimeto in letteratura. [↩]
- La nota stessa. [↩]
- In italiano “equal” è traducibile sia con “equabile” che “equalizzato”. [↩]
- Trasposto in ottave rispetto alla fondamentale. [↩]
- Non bisogna confondere il monocordo degli esperimenti con il monocordo strumento musicale. Il primo è uno “strumento da laboratorio” ed ha una sola corda; il secondo è un vero e proprio strumento musicale ed è composto da più corde identiche, della stessa lunghezza e accordate sulla stessa nota. [↩]
- Rispetto al Temperamento Equabile 12-TET [↩]